Introduction
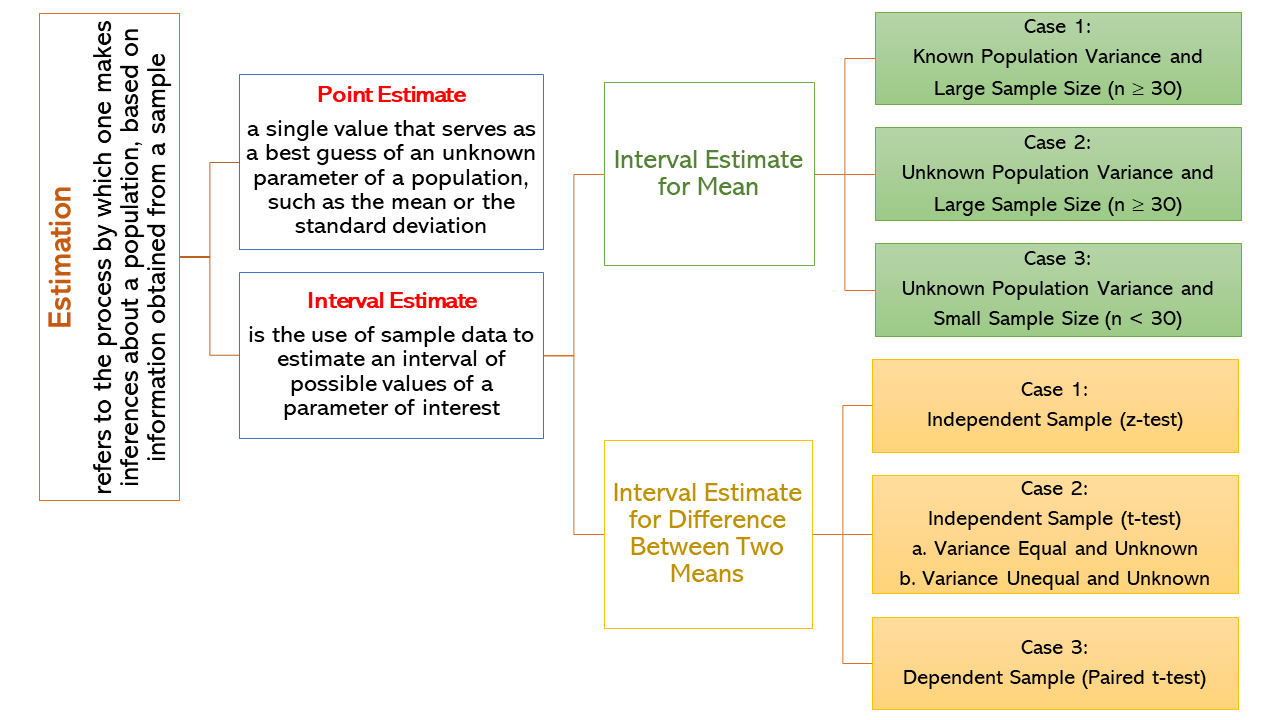
Estimation refers to the process by which one makes inferences about a population, based on information obtained from a sample. In this situation, a sample is selected from a population and data gathered from the sample will be used to estimate the parameter of a population. The relationship between estimation, estimate and estimator is that estimation is the process of finding an estimate of a parameter using an estimator. There are two types of estimation: point estimate and interval estimate.
A point estimate in statistics is a single value that serves as a best guess of an unknown parameter of a population, such as the mean or the standard deviation. It is calculated from sample data using a point estimator, which is a function that maps the data to the point estimate. The accuracy of a point estimate is not known precisely, but it can be improved by increasing the sample size. Point estimates are often used in other statistical calculations, such as confidence intervals.
Interval estimation in statistics is the use of sample data to estimate an interval of possible values of a parameter of interest. This is in contrast to point estimation, which gives a single value. Intervals are commonly chosen such that the parameter falls within with a 95 or 99 percent probability, called the confidence coefficient.
Interval Estimate for a Mean
An interval estimate for a mean is an interval of values that is likely to contain the true population mean. The interval estimate for a mean is called a confidence interval. The interval estimate is constructed using a point estimate and a margin of error. The margin of error is calculated using the standard error of the point estimate. The common confidence level used in research are 90%, 95%, and 99%.
Confidence Interval for a Mean
Case 1: known \(\sigma\) and large sample size \(n\ \ge\ 30\))
\[ \bar{X} - z_{\frac{\alpha}{2}}\ \large{(\frac{\sigma}{\sqrt{n}})}\ \lt\ \mu\ \lt\ \bar{X} + z_{\frac{\alpha}{2}}\ \large{(\frac{\sigma}{\sqrt{n}})}\ \ \ or\ \ \ \bar{X} \pm z_{\frac{\alpha}{2}}\ \large{(\frac{\sigma}{\sqrt{n}})}\ \]
References: